베지어 곡선

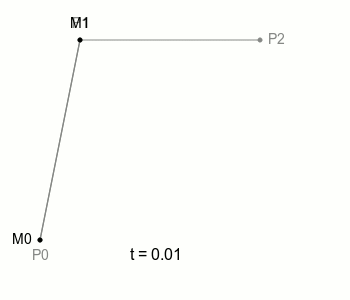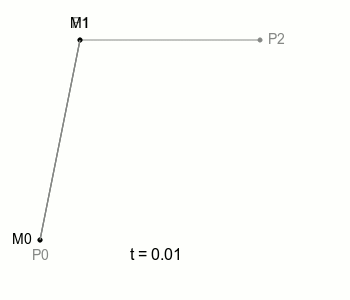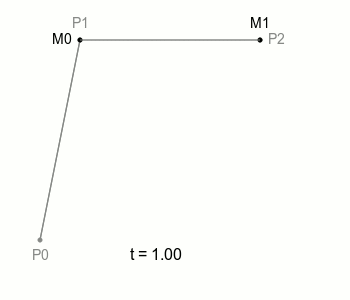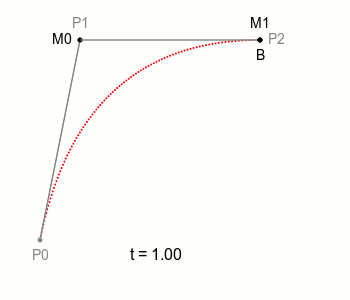
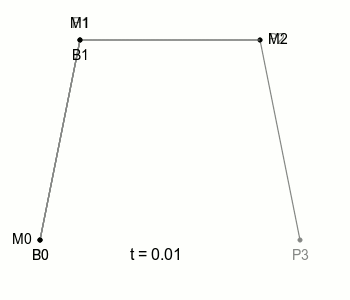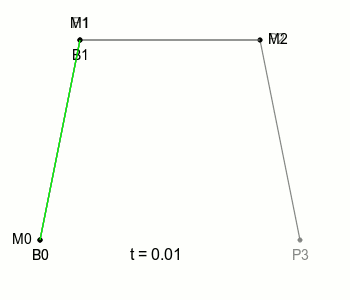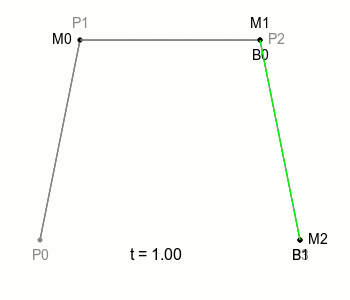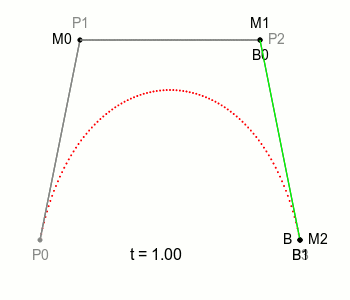
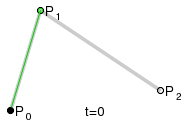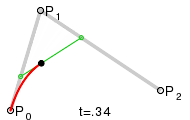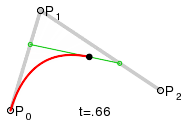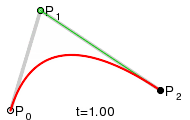
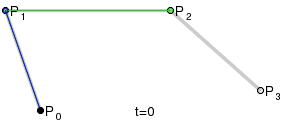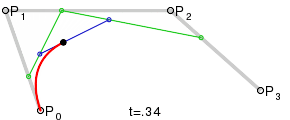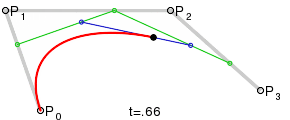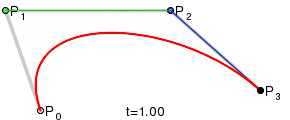
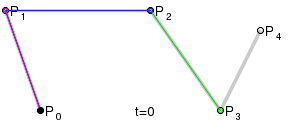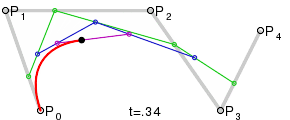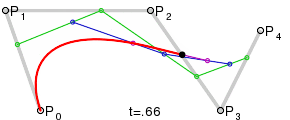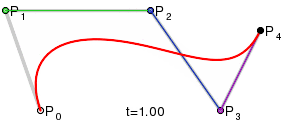
두 직선의 연장선이 만나는 점을 제어점으로 했을 때, 가장 자연스러운 2차곡선이 나옵니다. 본문에서는 왜 그렇게 되는지 단계별로 살펴봅니다.

자연스러운 곡선

우리는 2차 방정식이 자연스러운 곡선을 만드는데 효과적이란 사실을 발견할 것입니다.

자연스러운 곡선을 찾아보세요.

아래 직선을 연결하는데 가장 자연스러운 곡선을 고르시오.

원의 연결이 자연스럽지 않은 이유에 대해서 생각해 봅니다.
다음과 같은 상황을 고려해 보아야 합니다.

좌측 연결선의 기울기는 -1, 우측 연결선의 기울기는 0이 되어야 합니다.
점(-50, -25)과 원점(0, 0)을 지나야 합니다.

좌측 기울어진 직선의 방정식은, \[ y = -x - 25\] 우측 평행선의 방정식은, \[ y = 0\] 이를 자세히 그리면 다음과 같습니다.

보이십니까? 불편한 지점이? 애초에 삼각형((-50,25), (-25,0), (0,0))의 외접원이 y축 위에 있지 않기 때문에 두 점에서의 기울기를 모두 만족하는 원은 존재하지 않습니다.

미분값과 자연스러움

그렇다면, 왜 2차함수의 그래프는 자연스러워보이는지에 대해서 이야기 해볼 필요가 있습니다. 해당 대상을 지나는 이차방정식의 다음 조건을 만족해야 합니다.

꼭지점이 (0,0) 입니다.
(-50, 25)를 지납니다.

따라서 해는:

\[y=kx^2, k=\frac{1}{100}\] \[y'=\frac{1}{50}x \]

즉, 이차방정식에서는 (-50, 25)에서 기울기가 정확히 -1이었다가 (0,0)에서 0이 됩니다. 이를 그래프로 나타내면 아래와 같습니다. 보라색 미분박스에 주목합니다. 녹색은 원으로 구현했을 때의 그래프이며, 주황색은 2차함수로 구현됬을 때의 미분 값을 의미합니다. 원으로 구현했을 때, (-50, 25)에서의 대략기울기는 -1.15413이고 actan으로 계산하면 약 49.09도 즉 4.09도의 오차가 발생합니다. 따라서 아래로 약간 삐져나오는 모습으로 보이게 되는 것입니다.

베지어 곡선

우리는 '2차 베지어 곡선'과 '2차 방정식'이 같다는 것을 알 것입니다.

감 잡기

베지어의 설명들을 나타내는 그래프를 나열하자면 아래와 같습니다. ^{[1] [2]}

1차식

2차식

3차식

2차식

3차식

4차식

❮ ❯

다음 사이트^[4]에서는 재미있는 시뮬레이터를 만들어서 실습이 가능하도록 하고 있습니다. 직접 들어가서 시현해봅니다. 다음은 그 중 일부만 발췌해 봅니다.(주황색 점을 드래그 해서 다른 곡선을 만들어 보일 수 있습니다.)

반면 한국 위키의 베지어 곡선의 방정식을 보면,와 같이 나옵니다.^[3]

\[ P\left(t\right)=\sum_{i=0}^{n}B_{i}J_{ni}\left(t\right) \] \[ J_{ni}\left(t\right)=\pmatrix{n\\i}t^i\left(1-t\right)^{n-i} \]

~~바로 책을 덥고 싶어집니다.~~ 위 정의를 명시적 정의라고 합니다. 명시적 정의가 나온 이유는 중간점 B가 유한개 있다고 가정하고 B를 이항계수(파스칼 삼각형)으로 처리하기 위함이고, \( \pmatrix{n\\i} \)는 베르누이 다항식 일반입니다. n개중 i개를 순서 구분없이 골랐을 때 경우의 수를 나타냅니다.

\[ \pmatrix{n\\i} = \frac{n!}{i!(n-i)!} \]

이 식은 모든 베지어 곡선을 정의하기 위해서 나타난 것이고, 우리는 간단한 것(2차식), 그리고 그것중에서도 더 간단한 것(특수한 경우)를 알아보겠습니다.

중선정리

분명 중선정리인데, 어째서 2차식이 되고, 어째서 중선과 관련된 방정식이 존재하지 않는지 의문이 듭니다. 참고로 중선의 방정식은 아래와 같습니다.

\[ P(x,y) = (\frac{mA_x + nB_x}{m+n}, \frac{mA_y + nB_y}{m+n})\]

즉, 중선의 중선의 값이 \(Q_i\)의 값이 됨을 알 수 있고, 이를 수식으로 풀면:
(2차 베지어 함수이므로 Q, 3차는 C로 정의하겠습니다)

\[ A'(x,y)=\left(\frac{mA_{x}+nP_{x}}{m+n},\frac{mA_{y}+nP_{y}}{m+n}\right) \] \[ B'(x,y)=\left(\frac{mP_{x}+nB_{x}}{m+n},\frac{mP_{y}+nB_{y}}{m+n}\right) \] \[ Q(x,y) = \left(\frac{m\frac{mA_{x}+nP_{x}}{m+n}+n\frac{nB_{x}+mP_{x}}{m+n}}{m+n},\frac{m\frac{mA_{y}+nP_{y}}{m+n}+n\frac{nB_{y}+mP_{y}}{m+n}}{m+n}\right) \]

여기서 m+n=1이라 가정하면, n은 전체100%중 남은 비율(거리)이라고 의미가 부여됩니다.

\[ Q_x = (1-n)^{2}A_{x}+2(1-n)nP_{x}+n^{2}B_{x} \] \[ Q_y = (1-n)^{2}A_{y}+2(1-n)nP_{y}+n^{2}B_{y} \]

단순2차 함수

아래의 그래프에서는 \(B = (-A_x, A_y)\), \(P = (0, -A_y)\)가 됩니다.

\[ Q_x = (1-n)^{2}A_{x}-n^{2}A_{x} = (1-2n)A_x\] \[ Q_y = ({(1-n)}^{2}-2(1-n)n+n^2)A_y = (4n^2-4n+1)A_y = (1-2n)^2A_y\]

A가 \(y=kx^2 \)위의 점이라면 \( Q_y = k((1-n)A_x)^2 \)이 되므로 Q점도 항상 \(y=kx^2 \)위에 있게 됩니다.
2차식을 그릴 때, 각 선의 연장선(미분값이 같아지는 값)이 만나는 점을 선택하면 언제나 가장 완벽한 2차 방정식의 그래프를 그린다는 것에 있습니다.

좌표계를 회전시켰을 때, A B를 지나는 2차식은 무한하고, A에서 직선AP와 기울기가 같고, B에서 직선BP와 기울기가 같은 직선이 유일하다는 것은 매우 자명합니다. B는 A와 y축에서 항상 대칭이 아니더라도 B가 2차식 위에 있다면, Q가 언제나 2차식 위에 있다는 것을 증명하는 것은 그리 복잡한 일은 아닐 것입니다. 됩니다.

일반식의 유도과정

우리는 이차식을 그릴 때, 중간 점 Q의 x좌표를 다음과 같이 구했습니다.

\[ Q_x = {\color{red}(1-n)^{2}}A_{x}+{\color{blue}2}{\color{red}(1-n)n}P_{x}+{\color{red}n^{2}}B_{x} \] 이를 3, 4, 5차식으로 표현하면 다음과 같습니다. 그냥 기계적으로 전개한 결과물입니다. \[ Q_x = {\color{red}(1-n)^{3}}A_x + {\color{blue}3}{\color{red}(1-n)^2n}P_{1x} + {\color{blue}3}{\color{red}(1-n)n^2}P_{2x} + {\color{red}n^{3}}B_x \] \[ Q_x = {\color{red}(1-n)^{4}}A_x + {\color{blue}4}{\color{red}(1-n)^3n}P_{1x} + {\color{blue}6}{\color{red}(1-n)^2n^2}P_{2x} + {\color{blue}4}{\color{red}(1-n)n^3}P_{3x} + {\color{red}n^{4}}B_x \] \[ Q_x = {\color{red}(1-n)^{5}}A_x + {\color{blue}5}{\color{red}(1-n)^4n}P_{1x} + {\color{blue}10}{\color{red}(1-n)^3n^2}P_{2x} + {\color{blue}10}{\color{red}(1-n)^2n^3}P_{3x} + {\color{blue}5}{\color{red}(1-n)n^4}P_{4x} + {\color{red}n^{5}}B_x \]

빨간색 규칙: 여기서 P1은 제어점1, Pn은 제어점 n을 나타냅니다. 우리가 m:n으로 중점을 정리할 때, m과 n이 기여도였던 것을 감안하면 0 < n, 1-n < 1이므로 기여도에 의해 언제나 작아진다는 점을 직관적으로 알 수 있습니다.
파란색 규칙: 파스칼의 삼각형입니다. 이를 베르누이 다항식으로도 작성 할 수 있습니다.

\[ \begin{aligned} P\left(t\right) &= 제어점(B_1)\times기여도1 + 제어점(B_2)\times기여도2 + ... + 제어점(B_n)\times기여도n \\ &=\sum_{i=0}^{n}B_i (파스칼-삼각형)n^{증가함}(1-n)^{줄어듬} \\ &=\sum_{i=0}^{n}B_i \pmatrix{n\\i}n^{증가함}(1-n)^{줄어듬} \\ &=\sum_{i=0}^{n}B_i \pmatrix{n\\i}t^i(1-t)^{n-i} ~~~ \{ t = 변화값 ~| ~ 0 < t < 1 \} \end{aligned} \]

삶과 곡선

부드러운 곡선에 대한 고찰을 하면서 부드러운 것인가는 과연 어떤 것인가를 고민해 봅니다.

그림에서 왼쪽은 베지어, 오른쪽은 원으로 제어하였습니다. 자연스러움이란 익숙한 것이라는 말이 있습니다. 현대에 와서 '황금비'는 유사과학이라고 밝혀졌지만, 분명 대세라고 느껴지던 시기가 있었고, 지금은 round가 아무래도 편한 느낌이 있습니다. 저는 아무래도 우측(round)가 조금 더 편합니다. round가 가능할 때는 round를 사용하고 그렇지 못할 때, 베지어를 사용할 것 같습니다.

그렇다고 round가 무적은 아닙니다. 2차식은 완만한 변화량의 변화를 보여주지만, 헨들이라고 가정했을 때, 한 순간에 일정 각도를 틀어야 하므로 현실적으로 불가능하거나 매우 위험합니다. 반대로, 원은 부드러운 각가속을 하기는 하지만 순간적인 회전량이 매우 클 수 있어서, 교차로에서 가이드 그대로 따라서 주행하면 동승자가 싫어할 수도 있습니다.

삶은 여러가지 부드러운 곡선을 요구합니다. 베지어 곡선에 최적의 추천 제어점을 찾는 알고리즘이 있으면 괜찮을 것 같습니다.